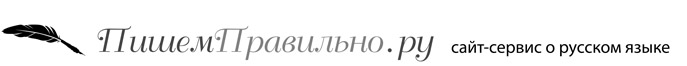Выражение гипотеза Пуанкаре вызывает интерес как её чрезвычайной абстрактностью, отвлечённостью от обыдённых представлений, так и тем, что окончательно доказавший её Г. Я. Перельман отказался от престижнейших международных наград за достижения в математике и прилагавшихся к ним миллионов долларов США. Однако всё ещё бытующее наивное пояснение, что, мол эта гипотеза (предположение) говорит, как без надрезов и проколов из шарика сделать бублик, или наоборот, неверно в принципе. Значение гипотезы Пуанкаре в целом сильнее и глубже:
- «Говоря простыми словами, гипотеза Пуанкаре утверждает, что изначальная геометрическая форма всего сущего – сфера, шар».
- «Ввиду особой важности для развития как фундаментальных наук, так и их практических приложений гипотеза Пуанкаре была включена институтом Клейна в число так называемых “задач тысячелетия”».
- «Полное доказательство гипотезы Пуанкаре затянулось почти на 100 лет: Анри Пуанкаре выдвинул её в 1904 г., а Перельман окончательно доказал в течение 2002 – 2003 гг».
- «На сегодняшний день гипотеза Пуанкаре является единственной решённой задачей тысячелетия».
Синонимы «задача Пуанкаре», «предположение Пуанкаре», «тезис Пуанкаре»; частичный «обобщённая гипотеза Пуанкаре» (для n-мерных топологических пространств).
Введение
Гипотеза Пуанкаре относится к одному из самых абстрактных разделов математики – топологии. Эта наука изучает самые основные, фундаментальные свойства геометрических тел (фигур), которые в ней называются в общем многообразиями, чтобы не путать с множествами в не менее абстрактной теории множеств; в сущности же каждое топологическое многообразие это в то же время и конечное множество в пространстве, которое может быть объединением (грубо говоря, суммой) нескольких других множеств. Множество, в свою очередь, это в самом общем смысле совокупность единичных объектов, схожих по какому-то признаку. Так, кубик состоит из множеств сторон (6 элементов), рёбер (12 элементов) и вершин, или углов (8 элементов). Компактным называется многообразие, замкнутое и ограниченное в пространстве независимо от того, есть у него края и концы, или нет. У шара нет ни конца, и края, но он компактен, как и кубик.
Основная, так сказать, производственная операция в топологии – деформация, причём имеется в виду пластическая деформация, не приводящая к разрывам и/или образованию на теле чего-то острого – концов (остриёв), рёбер, краёв. То есть, участков поверхности, кривизна которых возрастает до бесконечности; в топологии такие точки или линии называются сингулярностями. А в остальном тело можно сжимать-растягивать, изгибать, скручивать как угодно (вверху на рис. ниже) – в топологическом смысле оно остаётся тем же самым.
Если сингулярностей на теле изначально не было, то оно считается гладким, пусть даже оно всё в буграх, ямках и морщинах, лишь бы плавных, без изломов и разрывов, которые есть сингулярности. Говорят также, что у такого тела гладкая метрика, а если в процессе деформации сингулярностей не появилось, то у этого тела метрика сохраняет гладкость или же его метрика остаётся гладкой.
Примечание: метрика тела или пространства, в котором оно находится это его общее геометрическое описание. Когда вы говорите «шар круглый, а кубик угловатый», вы тем самым даёте им банальные словесные метрики.
Так вот, топология занимается самыми основными свойствами тел. Например, при любых корректных деформациях тора (бублика) дырка в нём остаётся (в центре на том же рис.). Корректная деформация здесь означает «не нарушающая гладкости метрики тела».
Одно из фундаментальных понятий топологии – гомеоморфность, или гомеоморфизм, что можно перевести как «единоформие». Гомеоморфными называются тела, имеющие одинаковый набор основных топологических свойств. Так, внизу на том же рис. спортивная гиря и заяц гомеоморфны друг другу – в них есть сквозное отверстие, дырка, как в бублике; у зайца это пищеварительный тракт. Но гиря с «ухом» для захвата не гомеоморфна цельнолитой гантели; а живой заяц – фарфоровому зайчишке; в тех сквозной дырки нет. Зато гантель и статуэтка гомеоморфны друг другу, даже если фарфоровая фигурка полая (см. опять вверху на том же рис.).
Следующее понятие – топологическая эквивалентность; это общее сходство по форме. Заяц топологически эквивалентен кошке, собаке и мыши, но не эквивалентен слону и акуле: у слона есть хобот, а у акулы нет ни его, ни носа, ни ушей и лап или ног. Поэтому слон и акула тоже не эквивалентны друг другу, хотя все животные, имеющие рот и задний проход, гомеоморфны друг другу.
Еще одно из топологических сходств – гомотопичность. Попросту её описать можно так: если при любых корректных деформациях тела любой из возможных путей на нём остаётся непрерывным, то данное тело сохраняет гомотопичность. А если мы из одного тела получаем другое при том же условии, то исходное и конечное тела будут гомотопичны друг другу, см. след. рис.
Некий неразрывный путь L из точки 1 на теле в точку 2 на нём же при деформациях тела может извиваться как угодно, хоть узлами завязываться, но, если он не рвётся – тело сохраняет гомотопичность исходной форме (фигуре). Однако, если найдётся хотя бы один путь, прерывающийся в результате деформации – гомотопичности тут нет. По аналогии в жизни: все безостановочные пути от Красной площади в Москве до Дворцовой в Санкт-Петербурге гомотропичны, даже если мы мимоходом проскочим Гренландию, Антарктиду и Австралию. А вот если свернём с прямой трассы перекусить и размяться – путь перестанет быть гомотропичным; остановка это его разрыв.
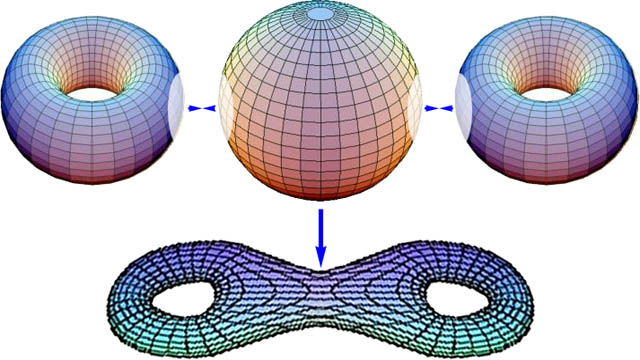
Теперь, связность тела. Если на нём возможно без отрыва от поверхности описать плавную замкнутую кривую (в «нашем» евклидовом 3-мерном пространстве – окружность), которую можно будет свести в точку так, чтобы она не теряла геометрического подобия самой себе, то это тело будет односвязным. К примеру, шар на рис. ниже односвязный, а вот тор – нет: на нём можно описать как минимум две окружности, в точку не сводимых.
Примечание: топология наука весьма и весьма общая, поэтому под «кривой» здесь подразумевается семейство или группа кривых, сводимых в точку, как круги на шарике на рис. Нетрудно понять, что на сфере возможно бесконечное количество таких групп (семейств) кривых, но несмотря на то, сфера всё равно остаётся односвязной.
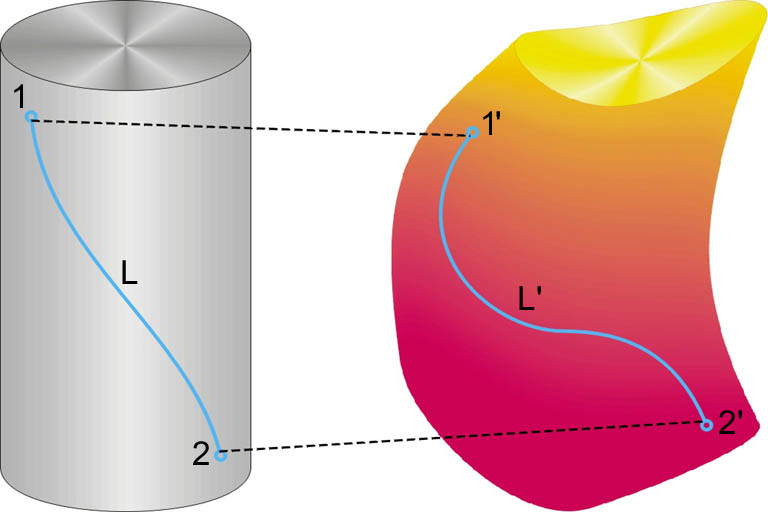
Понятие связности тела не следует путать с понятием связной суммы топологических многообразий, то есть объединения нескольких тел в одно. Связная сумма многообразий получается при помощи «вспомогательных» топологических операций: проколов, разрезов, склеиваний. Тела, объединённые в связную сумму, приобретают фундаментальные свойства слагающих её частей. Например, на след. рис. показано соединение в связную сумму сферы и двух торов.
Полученная фигура – сфера с двумя ручками – односвязна, на ней можно провести сводимую в точку окружность, и в то же время у неё есть две дырки. К слову, сфера с двумя ручками («шарик с ушами» или «наручники» на математическом жаргоне) широко используется в топологических выкладках.
Примечание: также широко используемый популяризаторами топологии пример – кружка, превращаемая в бублик и обратно – это связная сумма одной сферы и одного тора.
И наконец, такое фундаментальное понятие, как фундаментальная группа. Это общее количество плавных замкнутых кривых (точнее – семейств кривых) на многообразии, не сводимых в точки пластической деформацией. В трёхмерном евклидовом пространстве это, попросту выражаясь, количество сквозных дырок в теле. Для сферы с двумя ручками фундаментальная группа = 2; для чашки или кружки = 1, а вот для крутилок-спиннеров, по которым несколько лет тому назад буквально сходил с ума весь мир, фундаментальная группа = 3 или 4, в них было по 3 или 4 дырки. Для практики, если хотите, определите фундаментальную группу своего кухонного дуршлага. Не забудьте только и про дырочку в ручке, которой его вешают на крючок или гвоздик: занятия топологией требуют предельного внимания и сосредоточения на сути задачи. А порой и запредельного, к чему мы ниже и переходим.
Постановка задачи
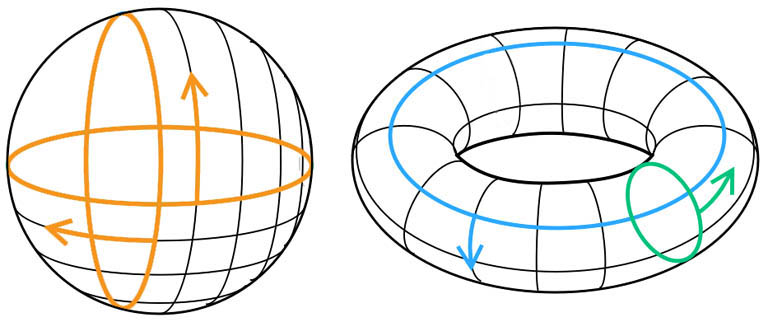
В топологии изначальными многообразиями, исходным фигурами, считаются сфера (шар) и тор (бублик). Кроме видимого наличия дырки, отличаются они также характером искривлённости поверхности: у сферы одна кривизна, а у тора две независимых друг от друга, см. рис.
Основное положение топологии гласит: сфера и тор не гомеоморфны, то есть превратить одно из этих тел в другое тривиальными преобразованиями (пластическими деформациями), невозможно: надо резать, колоть, кромсать на куски и уж тогда склеивать из них.
Такое положение сразу не понравилось учёным. Во-первых, из-за технических трудностей в применении к практическим задачам. Например, сферу можно рассекать плоскостями как угодно, и каждое сечение будет кругом. А произвольное (но, возможно, единственно допустимое в каждом конкретном случае) сечение тора плоскостями даёт различные фигуры, работать с которыми трудно, а порой и невозможно без применения громоздких, дорогостоящих и по существу своему не абсолютно надёжных численных методов.
Во-вторых, в логико-философском плане: не гомеоморфность сферы и тора давала повод для сомнений в исходном единстве всего сущего. А отсюда недалеко и до «научно обоснованного» расизма, и даже до утверждений, что, дескать на самом деле дьявол это бог, а зло есть добро. Математика, она же обо всём и во всём; сфера и тор в ней одинаково важны, и никто никак не может доказать, что из них «лучше», а что «хуже», что «доброе», а что «злое».
Жюль Анри Пуанкаре (1854 – 1912) был последним на сегодняшний день даже не математиком – теоретиком-универсалом. Топология как особая наука это, между прочим, его творение, а в создании специальной теории относительности (СТО) он лишь ненамного отстал от Альберта Эйнштейна, причём последний использовал математический аппарат, разработанный именно Пуанкаре.
Так вот, Анри Пуанкаре, закладывая основы топологии, и выдвинул гипотезу, строго формулируемую так: «Всякое n-мерное многообразие гомотопически эквивалентно n-мерной сфере тогда и только тогда, когда оно гомеоморфно ей», это и есть точная формулировка обобщённой гипотезы Пуанкаре для пространств любой целой размерности (у фракталов размерности дробные). Для нашего 3-мерного пространства формулировка такая: «Всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере»; под «краем» здесь понимается сингулярность в смысле, описанном выше: край как таковой, излом, ребро, остриё. Это уже формулировка гипотезы Пуанкаре в том виде, в каком она вошла в задачи тысячелетия.
Хотите – разбирайтесь сами, что это значит простыми словами; необходимые для этого определения даны выше. А нет – даём подсказку: «Любое реальное тело, занимающее определённую не бесконечно большую область пространства, можно расчленить на конечное количество не бесконечно малых шариков и, если надо, собрать из них же другое тело, равное исходному по объёму».
Обратите внимание: в таком определении уходит условие гладкости тела «без края». Основание – ничто в этом мире не может быть меньше так называемой планковской длины lp = 1,616225(18)x10–35 м, и радиус кривизны тоже. Следовательно, «идеальных сингулярностей» просто-напросто не бывает, а любое реально существующее тело в той или иной степени округло. По этой же причине действие гипотезы Пуанкаре допустимо распространять на области пространства, заполненные силовыми полями.
То есть, Пуанкаре – математик (его двоюродные братья Раймон и Люсьен также известные личности) принял как постулат единую первооснову мира и предположил, что от якобы неразрешимого противоречия между сферой и тором можно избавиться, идя кружным путём.
Примечание: современные теории не запрещают прямо существования миров на иной физической основе, но, если таковые когда-нибудь обнаружатся, для них и вся наука нужна будет другая, а пока нет, то и рассуждать об этом нет смысла.
Современники вначале не восприняли гипотезу Пуанкаре всерьёз, посчитав её скорее философским, чем математическим построением. Да и не до того им было: изобретение радио (1895), квантовая теория Планка (1900), начало авиации (1903), СТО (1905); затем – Первая Мировая война и революция в России, ОТО (общая теория относительности, теория относительности Эйнштейна), фашизм, нацизм и т. д. В научной среде ходили слухи, что Пуанкаре в последние годы жизни жаловался, что никак не может найти доказательство своей гипотезы для n = 3, но его доказательств для других случаев никто никогда не видел. Так что, начиная с середины 30-х предположение Пуанкаре доказывалось по частям, для n = 2, 4 и 6, и >5. К началу XXI в. недоказанным оставался только самый важный для нас случай для n = 3, то есть для того мира, в котором мы живём.
Доказательство
Путь к полному решению гипотезы Пуанкаре нащупал Р. С. Гамильтон где-то в середине 60-х прошлого века. А именно: ориентироваться по так называемому потоку Риччи на подходе к сингулярности. Поток Риччи это в общем система дифференциальных уравнений в частных производных, похожих на уравнения теплопроводности. Физический их смысл не так уж сложен: поток Риччи описывает перераспределение внутренних напряжений в теле при его деформации; если же содержимое тела текучее, то и реальные его перетоки, перетекание из места в место в пределах тела, как в наполненном водой пластиковом пакете, который мнут руками.
Идея Гамильтона также не очень-то сложна, а самая её суть обозначена ещё геометрами древности: «Нет геометрии без твёрдых тел», то есть геометрия пустых мест бессмысленна. В настоящее время под древним «твёрдым телом» подразумевается область пространства, наполненная материей – веществом или физическим полем, например, электромагнитным излучением.
Итого способ, предложенный Гамильтоном, таков: растягиваем тело на гомеоморфные сфере части, связанные бесконечно тонкими канальцами, и разрезаем их. Поскольку через бесконечно малую дырочку ничего из фрагмента тела не выйдет и ничего снаружи в него через неё не войдет, то разреза как бы и не было, и мы «не выходим за пределы дозволенного», то есть якобы обходимся пластической деформацией.
Гамильтон не справился с поставленной им же задачей: ему никак не удавалось сохранить гладкость метрики, то есть после разреза оставались острия, как «хвостики» пластилинового шарика, который разрывают пальцами. Всё это было, разумеется, «на бумаге», в теоретических выкладках.
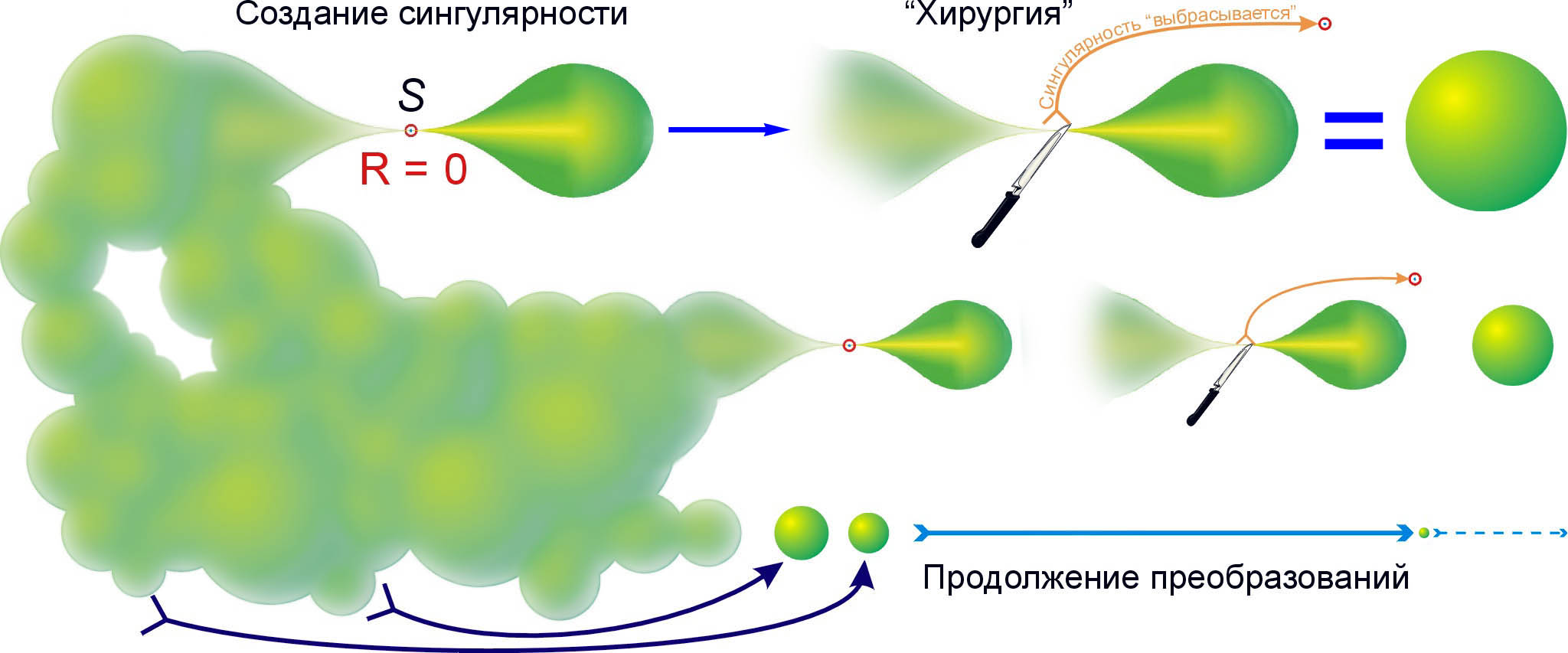
О работах Гамильтона Г. Я. Перельман знал, но его неоценимая заслуга в том, что он нашёл-таки способ вырезать из «ниточки» сингулярность, и только её, и заклеить бесконечно узкую дырочку такой же бесконечно малой сферой (см. также рис.):
- Пусть перед нами некая совершенно неописуемая масса материи, что-то вроде дырявой амёбы. «Защипываем» её кусочек и оттягиваем до тех пор, пока тяж между нею и остальным вот-вот порвётся – мы создали сингулярность.
- В банальном понимании сингулярность это бесконечно малая область пространства, математическая (и физическая) точка, в которой связанный с её размером параметр приобретает бесконечно большое значение величины; так сказать, или уплотняется, или разгоняется до бесконечности.
- По идее, поток Риччи через сингулярность становится бесконечно большим, на этом, кажется, и запнулся Гамильтон: тело мгновенно вытечет через разрез, и какие уж тут деформации – нет тела, нет дела, и вся геометрия на том и кончается.
- Перельман придумал «поток Риччи с хирургией» – способ остановить его в сингулярности, сделать нулевым.
- Всё, теперь можно вырезать и выбрасывать сингулярности – как это сделать, не трогая собственно тела, нашёл тоже Перельман, а заклейка дырочек шариками в топологии уже известна. Метрика при этом остаётся гладкой: мы как бы «замазываем» полое остриё, образно выражаясь, будто бы запаиваем или зачеканиваем кончик иглы шприца прежде, чем двинется его поршень.
- Раз разом повторяя преобразование, получаем набор сфер, суммарный объём которых в точности равен объёму исходного тела. «Отщипывать» можно как от одного и того же места, так и от разных по очереди. Следовательно, любое гладкое геометрическое тело можно представить в виде комплекса сфер, соединённых трубочками, что и требовалось доказать. Гипотеза Пуанкаре окончательно доказана, теперь она полноправная теорема.
- Сборка новой фигуры – обратным порядком: растягиваем шарики, делаем «хирургию», но «хвостики» не заклеиваем, а склеиваем друг с другом. Полученную цепочку, или ожерелье, или гроздь, или кисть, или что-то ещё мнем и тискаем до желаемой конфигурации.
Примечание: в популярных описаниях потока Риччи с хирургией встречается утверждение, что в ходе его применения «выбрасывается всё». На самом деле «выбрасывается» фундаментальная группа исходного тела – у сферы она = 0; следовательно, и у набора сфер тоже = 0. И обратно, собирая из этих же сфер кольца, можно создать новое тело с заданной наперёд фундаментальной группой.
И что это всё значит?
Топологические теоремы как правило не имеют прямого выхода в практику, но топологические методы и подходы с успехом используются едва ли не во всех областях человеческой деятельности. Что касается задачи Пуанкаре, поясним на примерах.
Пример 1
С точки зрения топологии, растения и одноклеточные микроорганизмы – сферы, шары. Животные со сквозным пищеварительным трактом – торы, «бублики». Но есть и животные – «топологические шары», у которых заднего прохода нет и никогда не было; к примеру, кишечнополостные (медузы, коралловые полипы, и т.п.), плоские черви (планарии) и др. Едино ли происхождение всего живого на Земле?
После доказательства гипотезы Пуанкаре сомневаться в единооснове земной жизни нет причин: вся совокупность прочих данных биологии указывает на это. А если бы оказалось, что предположение Пуанкаре неверно хотя бы в одном случае, то множеству биологов высшей квалификации пришлось бы оставить жизненно важные дела (борьбу с болезнями, глобальную продовольственную проблему, экологию), чтобы заняться первоосновами своей науки. Ибо без неё и выход в практику будет малоэффективен, как здание без фундамента неустойчиво.
Пример 2
Всё разнообразие взаимоотношений между людьми – межличностных, общественных, межгосударственных – возможно представить как топологическое многообразие в некотором p-мерном пространстве. Следствие из полного доказательства гипотезы Пуанкаре данном случае однозначно: все проблемы в отношениях между людьми могут быть решены плавно, эволюционным путём, или же, в крайнем случае, точечным, ничтожно малым и потому безболезненным воздействием. А революции, войны, истребления каких-то «не таких», «не своих», «неправильных» и прочие «великие и ужасные» деяния того же разбора – исторические ошибки вследствие недопонимания чего-то важного. Попросту – не углядели, где тут кроется сингулярность в отношениях, ну и пошло, хлынул поток. Теоретически – Риччи, а реально – кровавый или же оскорблений, инсинуаций, травли, запретов, санкций и прочих средств подавления неугодных.
Пример 3
К настоящему времени ясно, что ни «зелёная», ни водородная энергетика экологических проблем не устранят: их массовое внедрение сопряжено с уймой технических неувязок, по сравнению с последствиями которых дым от сжигания бурого угля или сырой нефти покажется воздухом в карельском сосновом бору. «Озеленяться» у себя дома, заодно жирея на экологических пошлинах, по большому счёту бесполезно: климат у нас у всех общий. Не мешало бы подумать об этом тем, у кого нет плачевного опыта «построения коммунизма в одной отдельно взятой стране». Но вернёмся в тему.
Выход из положения – управляемый термояд, термоядерная энергетика, а на протяжении переходного периода – ядерная с экономичными и безопасными реакторами на быстрых нейтронах; топлива для них хватит не на одну сотню лет. Токамак ИТЭР вроде бы окончательно собираются запустить в 2024 году, но, к сведению читателей: ток в сеть он давать не будет, этот термоядерный реактор строится для исследований термояда уже в промышленно-технологическом плане. Почему?
Потому что к экономически оправданному термояду просто так не подступишься, уж больно капризная она, плазма в реакторе. Общая беда токамаков с тороидальной реакционной камерой – очень низкий коэффициент использования плазмы. Электричество от токамаков с «бубликами» стало бы непомерно дорогим, а массовое строительство подобных колоссов – неподъемным для глобальной экономики.
Токамаки со сфероидальной камерой, над которыми сейчас усиленно работают в России, экономичнее, компактнее и дешевле. Но сфероид не сфера, их камеры это просто сильно обжатые со всех боковых сторон торы; центральный «столбик» в них остаётся.
Токамак с «настоящей» сферической камерой был бы ещё лучше, но с ним серьёзнейший вопрос: а можно ли добиться нужной устойчивости плазмы в сфере без центральной «колонки»? Доказательство гипотезы Пуанкаре дает на него в общем положительный ответ. Без технических деталей, но по крайней мере понятно, что работать в этом направлении имело бы смысл.
И это ещё не все
Тем не менее, не исключено, что глубинное значение абстрактных построений Г. Я. Перельмана ещё важнее. Мне (автору этой статьи) его доказательство кажется несколько натянутым: резать ведь все же нужно. Хотя, конечно, лучше неощутимый разрез, чем повальная резня в любом смысле слова.
Более существенным представляется другое: не хотелось бы ошибиться, но Григорий Яковлевич, похоже, едва ли не первый из людей, осознанно и целенаправленно работающий с сингулярностями, и использующий по меньшей мере одну из них для определённой цели.
Дело в том, что теоретики боятся сингулярностей как чёрт ладана. Появление сингулярности в теории означает: здесь – стоп! Отсюда и глубже эта штука не работает, непригодна для этого.
Например, ОТО (теория относительности Эйнштейна) не дает никаких инструментов для работы с сингулярностями, которые сама же плодит. Долетели до горизонта событий – и всё, нет никаких способов понимания, есть ли за ним что-либо и что там с чем творится. Рассуждения о «гиперпереходах», «подпространстве» и т.п. – ну, это для фантастики эпохи «железных людей на стальных звездолётах» и любителей псевдонаучных спекуляций.
А тут, понимаешь ли, некий ранее никому не ведомый математик берёт, да и обращается с сингулярностью, как лаборант с колбой или вольтметром. Если вдуматься, то напрашивается вывод: в данном случае человек своим разумом превзошёл возможности человеческого разумения как такового. Что даёт надежду на то, что и остальные задачи тысячелетия будут когда-то да решены. Потому как без ясных и точных ответов на них каждый следующий шаг фундаментальной науки становится всё короче и обходится всё дороже во всех смыслах.
***
© ПишемПравильно.ру
Автор: Садов Артур Александрович, лингвист-типолог
Перечень академических источников, использовавшихся при подготовке материалов.