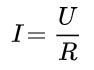Прежде всего: в словосочетании «закон ома» оба слова можете писать с малой буквы, только если вы неверующий, но интересуетесь буддийской теологией. А в специальном термине «закон Ома» второе слово пишется с большой, так как это фамилия его открывателя – немецкого физика Георга Ома (Georg Simon Ohm) в русском написании. Буддисты всё слово «ОМ» пишут большими буквами, оно у них сакральное (священное), см. далее. Но и помимо сакральных верований значение выражения «закон Ома» не ограничивается школьной физикой и электротехникой. Стандартная формлировка закона Ома такова:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.
Формула:
где:
I — сила тока в цепи, А;
U — электрическое напряжение на участке цепи, В;
R — электрическое сопротивление участка цепи, Ом;
- «Закон Ома для полной цепи это основной закон электротехники, описывающий прохождение электрического тока по контуру, состоящему из источника электроэнергии и её приёмника (потребителя)».
- «Закон Ома выведен по аналогии с гидродинамикой: чем шире просвет трубы (выше проводимость электросхемы, т.е. меньше её электрическое сопротивление), тем больший ток жидкости (электрический) она может пропустить, а чем больше напор (электрическое напряжение), тем сильнее будет ток».
- «На основе закона Ома в полной (интегральной) форме разработаны все остальные базовые законы электротехники».
- «Для расчётов электрических цепей переменного тока небольшой частоты и без существенного сдвига фаз (например, квартирной проводки) закон Ома пригоден без дальнейшей доработки».
- «На переменном токе повышенной частоты и в цепях с заметной реактивностью (сдвигом фаз между током и напряжением; несовпадением их максимумов и мгновенных (текущих) значений) используется закон Ома в комплексной форме».
- «Для расчётов резонансных цепей и/или на высоких частотах закон Ома непригоден».
- «В физике сплошных сред широко используется закон Ома в дифференциальной форме».
- «Кроме электрического закона Ома, в акустике и электроакустике применяется также акустический закон Ома, полученный тем же самым Георгом Омом».
- «Акустический закон Ома гласит, что сила звука пропорциональна квадрату колебательной скорости его источника, плотности среды и скорости распространения звука в ней».
- «Слышимая громкость звука равна логарифму его силы, рассчитанной по акустическому закону Ома, так как чувствительность человеческого уха нелинейна (мы рефлекторно вслушиваемся в слабые звуки и “приглушаем” громкие)».
- «Магнитный закон Ома, по которому рассчитываются магнитные цепи, просто назван в его честь, так как выведен братьями Гопкинс и потому в специальной литературе часто называется законом Гопкинса».
- «Магнитный закон Ома по смыслу и форме записи аналогичен электрическому: магнитная индукция в среде тем выше, чем больше напряжённость магнитного поля и магнитная проницаемость среды (её способность намагничиваться), т.е. чем меньше магнитное сопротивление среды».
Подробно разбирать все законы Ома мы не будем: базовый объясняют в школе, а производные от него – в вузах на спецкурсах. Но и «школьный Ом» не так-то прост, поэтому ограничимся пояснениями к нему с практическими выводами и примером, как его можно с пользой применить (и, возможно, подзаработать на этом). А уж потом примемся за ом, который, может быть ОМ, но не Ом.
Пояснение
Ом получил свой закон сразу для полной цепи из источника электричества и его приёмника (слева на рис.). Физический смысл его таков: источник электродвижущей силы (э.д.с.) E отдает энергию во внешнюю цепь. Если замерить напряжение на клеммах источника прибором с очень большим входным сопротивлением (см. ниже), то тем самым мы с достаточной для практики точностью определим его (источника) э.д.с. Мощность источника не безгранична, что учитывается «приписыванием» ему внутреннего сопротивления r: если замкнуть внешнюю цепь накоротко, то есть когда потерь энергии в ней не будет, то ток короткого замыкания получится Iкз = E/r.
Отсюда следует первый важный практический вывод: внутреннее сопротивление современных алкалайновых (щелочных) и литиевых гальванических элементов (которые в просторечии называют батарейками) очень мало, десятые и сотые доли ома. Также мало и входное сопротивление цифровых мультитестеров в режиме измерения тока. Поэтому не пытайтесь проверять батарейки тестером «на ток», как старые солевые: прибор, скорее всего, выдержит перегрузку экстратоком, в нём есть защита. Но батарейку наверняка «посадите»: литиевая всего лишь за секунду КЗ (короткого замыкания) теряет больше четверти заряда, а если «коротить» её дольше, то перегреется и может лопнуть, выбросив тучку отнюдь не полезных газов.
Примечание: ом – единица электрического сопротивления в системе СИ, названная в честь открывателя закона Ома. По-русски в электросхемах, а в текстах в сочетании с численным значением сопротивления пишется с большой буквы (напр. 27 Ом), но сама по себе – с малой. В языках, использующих латинский алфавит, Ом как единица сопротивления обозначается большой греческой буквой Ω. Проводник электричества, как известно, обладает электрическим сопротивление в 1 Ом, если по нему под действие разности потенциалов в 1 В (вольт) течёт ток в 1 А (ампер).
Далее, пропускная способность внешней цепи по энергии тоже не бесконечна, она оказывает сопротивление прохождению электротока, точно так же, как по водопроводной трубе не протечёт мгновенно бочка воды. Сопротивление прохождению электротока обозначается большой буквой R. В электротехнике, радиотехнике и электронике в качестве компонентов схем широко применяются специальные устройства с точно заданным электрическим сопротивлением – резисторы (от англ. to resist – «сопротивляться»). При прохождении тока электроэнергия нагревает и резистор, и соединительные проводники, и в конечном итоге рассеивается в пространстве.
Так как резистор сопротивляется току, то на нём (резисторе) должно быть некоторое падение электрического напряжения, или просто напряжение, иначе ток не потечёт. Аналогично: при нулевом напоре в водопроводе из крана ничего не вытечет, как его ни крути.
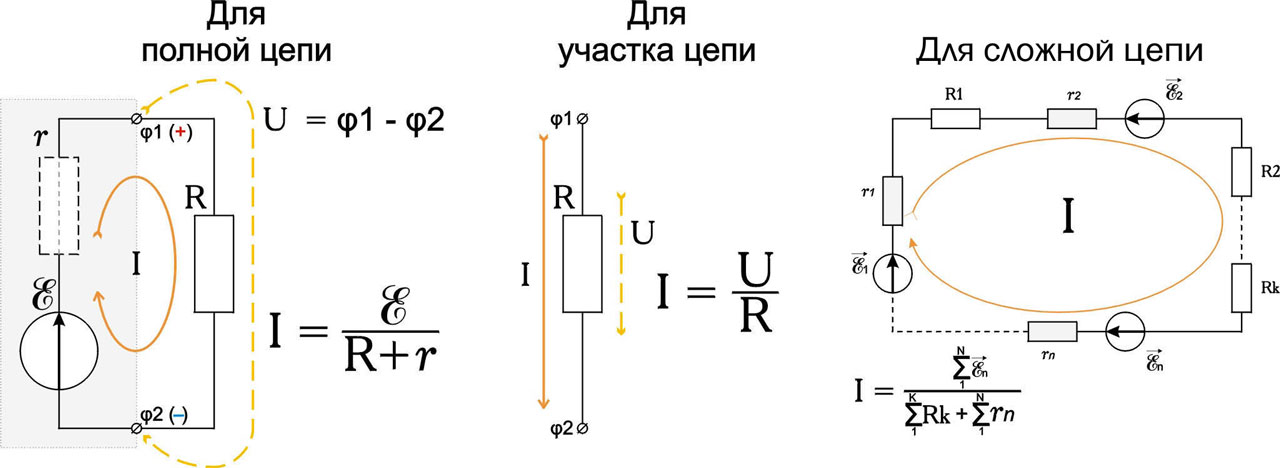
Цепь из источника, замкнутого на резистор, называется полной (опять см. слева на рис.). В полной цепи часть э.д.с. падает на внешнем сопротивлении (это напряжение источника под нагрузкой U), а часть – на внутреннем сопротивлении r. Ток в цепи при этом определяется формуле там же, слева на рис., которая и есть закон Ома для полной цепи. Его можно записать и так: φ1 – φ2 = IR = E – Ir, где φ1 – φ2 – разность электрических потенциалов на выводах (клеммах) источника.
На практике внутреннее сопротивление источников электричества стараются сделать как можно меньше, так как рассеивающаяся на нём энергия в любом случае пропадает зря. Так, внутреннее сопротивление бытовой электророзетки (которое, раз она не сама источник тока, называется выходным) – порядка мОм, то есть тысячных долей ома. А сопротивление, к примеру, ТЭНа стиралки на 2,5 кВт – 19 с небольшим Ом.
Практический вывод второй: не шутите с электричеством! Оно само по себе невидимо, неслышимо, не пахнет, но шарахнет – мало не будет.
Примечание: если Ом пишется с большой буквой М впереди, то это означает миллионы ом (мегом). Так, сопротивление резистора на 1,8 МОм (или 1,8 MΩ) = 1 800 000 Ом.
«Школьный Ом»
Поскольку выходное сопротивление источников электропитания обычно мало, то на практике их в большинстве случаев можно считать источниками э.д.с. (впрочем, см. далее). Отсюда вытекает «школьный» закон Ома для участка цепи (в центре на рис.). Другие формы его записи U = IR [а] и R = U/i [б]. Таким образом по двум известным значениям параметров участка цепи всегда можно найти недостающий: замерили напряжение на неизвестном резисторе и ток через него – вычисляем сопротивление по формуле [б]; нужно найти ток, если известно сопротивление и напряжение – берём формулу в центре на рис., и пр.
Например, предлагают вам с рук подержанный электрокамин. Не «выбьет» ли от его включения квартирный защитный автомат на 25 А? Замерили сопротивление, тестер показал 32 Ом. Току этот камин возьмёт I = U/R = 220 В/32 Ом = 6,875 А. Включать можно, но без стиралки и микроволновки. Потому, что, если при этом включится и бойлер, то защита сработает: 25 А и 220 В это 5500 Вт или 5,5 кВт. Обычная стиралка берёт 2,5 кВт; микроволновка 1,2 кВт; бойлер 1,5 кВт, итого 5,2 кВт, защита на пределе, остатка еле хватает на холодильник и телевизор, а мощность этого камина P = UI = 220 Вх6,875 А = 1500 Вт = 1,5 кВт.
Для сложной цепи
Когда-то в школах на дополнительных занятиях давали и закон Ома для сложной цепи. В сущности это второе правило (или закон) Кирхгофа, которое вообще-то учат уже в электротехнических вузах. Он легко получается из закона Ома для полной цепи, если применить векторное сложение источников э.д.с., о чём говорят стрелки над её обозначением справа на рис.
«Векторное» означает следующее: выбираем направление обхода цепи (обычно по часовой стрелке). Источники, которые дают ток по обходу, считаем с плюсом, а те, э.д.с. которых направлена против обхода – с минусом. Складываем таким образом все э.д.с., затем все внешние сопротивления, все внутренние, приплюсовываем друг к другу суммы сопротивлений, и по формуле закона Ома для полной цепи находим ток, только вместо значений отельных компонент в ней теперь будут их суммы по контуру.
Пример расчёта. Допустим, что справа на рис. у нас E1 = 12 В, E2 = 24 В, En = 60 В; R1 = 9 Ом, R2 = 14 Ом, Rn = 38 Ом; r1 = 2 Ом, r2 = 3 Ом, rn = 11 Ом. ΣE = 12 – 24 + 60 = 48 В. ΣR = 9 + 14 + 38 Ом = 61 Ом (сложение скалярное, не векторное, «арифметическое»!). Σr = 2 + 3 + 11 Ом = 16 Ом (сложение также скалярное). Получаем: I = ΣE/( ΣR + Σr) = 48/(61 + 16) = 48/77 = 0,62337… А.
Пример для практики
Буквально в последние годы полузабытый закон Ома для сложной цепи приобрёл неожиданную актуальность (см. также рис.).
Положим, вы домашний умелец и в свободное время подрабатываете ремонтом сведодиодных электролампочек. Современные их модели всем хороши, кроме одного – сгорают всё-таки гораздо чаще, чем хотелось бы, судя по их цене. Но примерно в 3/4 случаев отремонтировать неисправную «светодиодку» возможно.
Чаще всего выходит из строя один из излучателей, которые всё включены последовательно. То есть, найдя негодный, его можно просто закоротить – световой поток уменьшится ненамного, а общий ток через излучатели задаётся источником стабильного тока (ИСТ) в драйвере (или контроллере), спрятанном в цоколе.
Излучатели применяются одно- или двухкристалльные. Чтобы засветился одинарный, напряжение на нём должно быть не менее прим. 4 В; на двойной нужно подать вдвое больше. То есть, тестером излучатели не проверишь – напряжение на его щупах в режиме прозвонки менее 3 В.
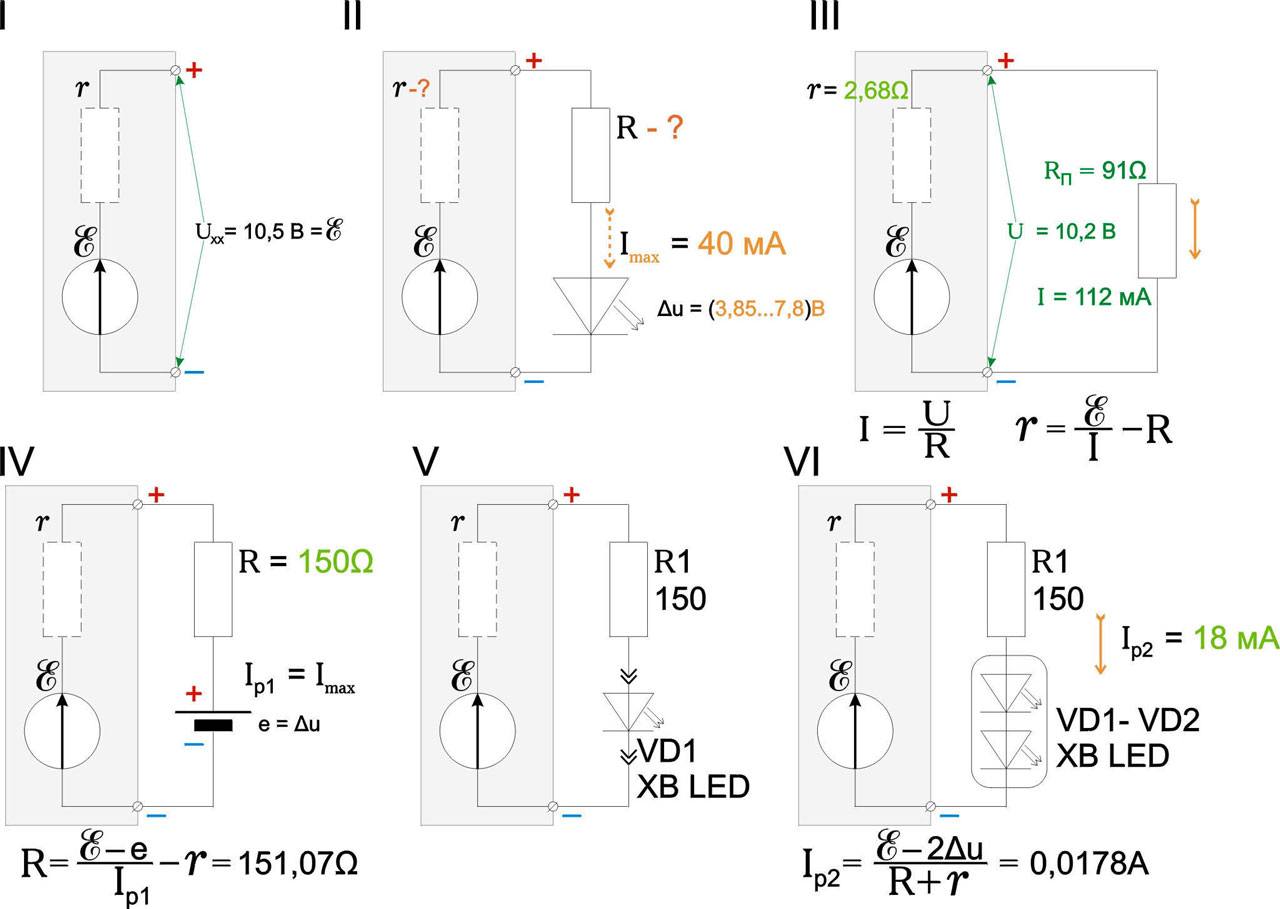
Ну, вы парень не промах, а в «загашниках» и вас нашлась зарядка для старого телефона. Вы домотали несколько витков к вторичной обмотке её трансформатора (это можно сделать, не выпаивая его), чтобы на выходе получилось напряжение холостого хода (без нагрузки) Uxx = 10,5 В (поз. I на рис.). До 12 и более повышать выходное напряжение не надо: там выпрямитель на диоде Шоттки, его таким вольтажем может пробить.
Но «тыкать» напрямую нельзя: максимально допустимый ток излучателей 60 мА, а переделанная зарядка по мощности может выдать больше 400 (исходные данные: 5,6 В; 800 мА). Что, ж звоним через ограничительный резистор на 1 кОм.
Однако вскоре обнаруживается незадача: некоторые отремонтированные лампочки очень быстро опять перегорают. Поиск и анализ причины приводит к выводу: помимо полностью негодного, там был и излучатель на грани полной деградации. Заменить на исправный возможно, но как найти «полудохлый»? По слабому свечению при прозвонке он не отличается от вполне исправных.
Итак, перед нами задача: рассчитать ограничительный резистор такой, чтобы на 100% выявлялись неисправные излучатели. Исходные данные к расчёту приведены на поз II; максимальный прозвоночный ток Imax берём в 1,5 раза меньше максимально допустимого, чтобы случайно не сжечь нетиповой излучатель.
Для начала нужно найти внутреннее сопротивление источника питания. Для этого нагружаем его током, примерно в 2 – 2,5 раза бо́льшим прозвоночного. Значение необходимого для этого пробного резистора Rп находим по закону Ома для участка цепи (формула [б]) выше. Подключаем нагрузку, меряем напряжение на выходе источника. Допустим, оно упало до 10,2 В (поз. III). По формуле модифицированного закона Ома для полной цепи (внизу справа на той же поз. III) находим внутреннее сопротивление источника r = 2,68 Ом; такой его величиной уже нельзя пренебречь.
Следующий момент: светодиодный излучатель – элемент сильно нелинейный, падение напряжения на нём слабо зависит от протекающего тока. Поэтому считаем его «батарейкой», включенной встречно источнику питания (поз. IV), и, видоизменив по правилам алгебраических выкладок формулу закона Ома для сложной цепи (внизу на поз. IV), сразу находим значение R; в щуп впаиваем ближайший по стандартному номиналу. Полученная схема пробника для проверки ультраярких светодиодных излучателей показана на поз. V.
Но пригодна ли она для проверки сдвоенных излучателей? Снова берём на вооружение закон Ома для сложной цепи, поз. VI. Прозвоночный ток выходит почти 20 мА – OK! На таком токе «живой» диод уже «полыхает», а «задохлик» тускло тлеет. Всё, довольно теории, за работу!
«Другой ОМ»
Вообще говоря, буддисты, когда пишут «ОМ», то или ленятся, или же не понимают догмата своей религии. Потому что правильно это их священное слово пишется АУМ. Такая последовательность исконных (утробных) звуков, согласно концепции буддизма, символизирует три первоначала Вселенной: Созидание, Поддержание (сущего) и Разрушение. Исходя из этого:
- «Закон ОМа (АУМ) в буддийском веровании утверждает: “Каждая мантра (сакральное заклинание) должна начинаться звуком АУМ (ОМ), иначе она не будет иметь божественной силы”».
***
© ПишемПравильно.ру
Автор: Садов Артур Александрович, лингвист-типолог
Перечень академических источников, использовавшихся при подготовке материалов.